Момент инерции — формулировка, свойства и методы решения

Одним из фундаментальных свойств физических тел является момент инерции. Люди с ним сталкиваются в повседневной жизни при езде на велосипеде или автомобиле, запуске различных механизмов, игре с мячом, катании на карусели и т. д. Изучают характеристику на уроках физики и сопромата. Знание этого параметра важно и в механике, особенно при нахождении силы, которая может привести тело к вращению.

Основные понятия и суть

- mi — масса в точке;
- rj — расстояние от точки до координаты.
То есть момент — это скалярная величина, являющаяся мерой инертности. В качестве единицы измерения по международной системе принято использовать произведение килограмма на квадратный метр (кг*м²). Обозначают параметр латинской буквой I или J. При умножении момента инерции на угловое ускорение можно определить сумму моментов всех сил, приложенных к телу: M = I * E. Фактически это уравнение является аналогом второго закона Ньютона.
М — это момент силы, оказывающий вращательное движение и воздействующий на ускорение тела, а E — угловое ускорение. Мера инертности тела отличается от массы тем, что вторая проявляется, когда его необходимо разогнать, а первая — при его раскручивании.
Вычисление параметра

Характеристика инерции тел зависит от их количественных показателей и формы. Для того чтобы найти характеристику, можно рассмотреть вращение материальной точки, находящейся на невесомой штанге, имеющей длину r и массу m. Для такой ситуации формулу момента инерции можно записать: I = m*r 2 . Длина r представляет собой радиус кольца, по которому происходит вращение объекта по оси. Таким образом, рассматриваемый момент зависит не только от массы тела, но и геометрических характеристик.
Любое тело можно описать совокупностью материальных точек. Для понятия процесса лучше всего рассмотреть простой пример. Пусть имеется невесомый цилиндр, способный вращаться по радиусу Rc. На него намотана верёвка, к которой приложена сила F. На цилиндр будут насаживаться тела с различной формой. Если известны его радиус и сила, с которой происходит раскручивание, то справедливо будет записать следующее выражение: M = F*Rc.
Допустим, на цилиндр помещены два тела. Одно имеет массу m1 и радиус вращения r1, а другое — m2 и r2. Используя основное уравнение динамики вращательного движения для первого тела с угловым ускорением ƹ1, момент силы можно определить как M1 = I1 * ƹ1. Соответственно, для второго предмета сила будет определяться по формуле: M1 = I2 * ƹ2.
Если эти два тела жёстко скрепить между собой, то они буду представлять собой составные части одного предмета, поэтому их угловые ускорения станут одинаковы (ƹ1 + ƹ2 = ƹ), а требующийся момент M станет равный сумме M1 + M2. Подставив значения, получим равенство M = I1*ƹ + I2*ƹ. Выражение можно упростить до вида M = ƹ (I1+I2). То есть нужный момент для тела, состоящего из совокупности точек, будет равен произведению суммы моментов инерции на угловое ускорение обоих тел.
Из сказанного можно сделать вывод, что момент инерции всего тела равен сумме моментов составных частей. Другим словами, он обладает свойством аддитивности. Используя это, можно составить алгоритм расчёта для любой формы.
Методика решения
Существует универсальный алгоритм, подходящий для расчёта параметра прямоугольника, треугольника, круга или другой фигуры произвольной формы. Допустим, есть сложное тело с заданной осью вращения. Необходимо найти момент его вращения. Для того чтобы решить поставленную задачу, используются два принципа:
- Аддитивность — свойство, обозначающее, что величина целого значения определяется суммой соответствующих ему частей.
- Формула нахождения момента для материальной точки I = m*r 2 .
Всё тело можно разделить на мельчайшие частички, которые представляют собой материальные точки. Номера этих кусков обозначают в виде i. Масса произвольной части будет определяться как дельта mi. Пусть этот кусок находится на расстоянии ri от оси вращения O. Для этой части момент вращения находится с помощью выражения Ii = Δ mi*ri 2 . Учитывая аддитивность, общий момент будет равен I = Σ Δ mi*ri 2 , где i принимает значение от 1 до n.
Эта формула является приближённой, так как точность зависит от массы частей и размера. Если кусочки, на которые разбивается тело, большие, считать их материальными точками нельзя. Чем мельче части, тем точнее будет результат. В соответствии с математическим анализом такие задачи решаются с помощью интегрирования. Понимая физический смысл момента инерции, можно отметить следующие зависимости:
- прямая пропорциональность массе;
- соответствие квадрату размера;
- изменение с учетом оси вращения.
Роль последнего пункта огромна. Например, если рассмотреть два момента вращения велосипедной спицы диаметром 2 мм и длиной 30 сантиметров, то можно увидеть зависимость от выбранной оси поворота.
Относительно вертикальной оси вращение обозначим I1, горизонтальной — I2. Подставив в формулы выражения, используемые для расчётов, можно получить отношение I1/I2 = (m*l2/12) / ((m*d2/8). После его упрощения будет верна запись I1/ I2 = (2/3)*(l/d)2. В итоге получится ответ 15000. Получается, если спицу будут закручивать с одинаковым моментом вокруг вертикальной оси и горизонтальной, то в первом случае она станет крутиться в 15 тыс. раз быстрее.
Моменты простейших объектов
Проведение интегрирования — довольно трудная операция, предполагающая хорошее знание высшей математики. Существует таблица, в которой собраны вычисления инерции для простейших геометрических фигур. При взятии сведений из неё важно обращать внимание на то, относительно какой оси приводится момент вращения объекта. Характеристика инерции для наиболее используемых объектов в физике имеет следующий вид:

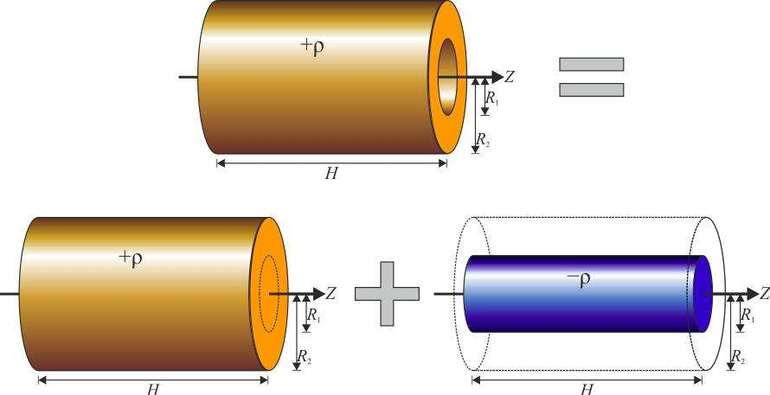
- Кольцо. Предположив, что точка имеет симметричное значение с противоположной стороны оси, можно утверждать, что формула не изменится. Если же точку распределить по плоскости перпендикулярной оси, то получится кольцо. Оно будет иметь такую же массу с кусками, находящимися на одинаковом расстоянии от центра r. Вычисление момента относительно оси вращения выполняют по той же формуле, что и для материальной точки: I = m * r 2 .
- Тонкостенный цилиндр. Нарисовав такую фигуру и указав на ней ось вращения, массу и радиус, несложно будет увидеть, что формула для нахождения момента будет аналогична кольцу.
- Диск. Вращение его происходит относительно оси, проходящей через его центр. Учитывая, что масса однородного диска распределена по всей его площади, то момент его будет меньше, чем у кольца. Проведённые расчёты показали, что момент диска будет меньше в два раза. Таким образом, формула выглядит как I = m*r 2 / 2.
- Сплошной цилиндр. Получают такую фигуру простым распределением массы сплошного диска вдоль оси. По аналогии с кольцом расчёт его характеристики инерции будет совпадать с однородным диском.
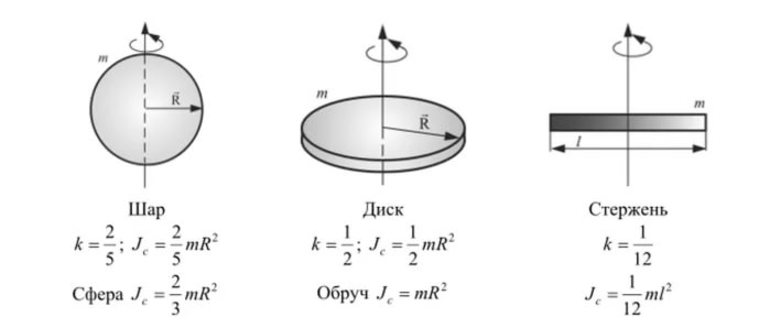
- Шар. Момент проходящей оси через центр тяжести равен удвоенному произведению m*r2, разделенному на 5: I = (m*r2) * 2/5.
- Сфера. Такой объект отличается от шара лишь тем, что внутри он полый. Направление вращения оси происходит через центр. Значение параметра для неё будет больше, чем шара, так как масса собрана не статически в одном месте, а размещена по всей поверхности. Расчёты показывают, что найти момент можно по формуле I =2*m*r2 /3.
- Стержень. Момент вращения проходит через центр вдоль оси, перпендикулярной стержню: I = (1/12) * m*L2. L — длина стержня.
При использовании этих формул необходимо учитывать, что единицей измерения момента инерции является кг* м², поэтому при расчёте величины следует приводить значения к этим единицам.
Теорема Гюйгенса — Штейнера

Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей. Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:
- Вычисления координаты центра масс: X = (m1*x1 + m2*x2+…+Mi*Xi) / (m1+m2+…+Mi) = (Σ Δ mi*ri 2 )/ m.
- Универсального расчёта инерции любого тела: I = Σ Δ mi*ri 2 .
Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.
Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).
В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r’.
Находится ri’ 2 по формулам для прямоугольного треугольника, в котором один катет равняется yi, а другой — xi — Oц. Значение ri’ совпадает с длиной гипотенузы. Таким образом, ri’ 2 = (xi — Oц) 2 + yi 2 . Подставив полученное равенство в формулу нахождения параметра момента в центре, можно получить следующую формулу: Io = Σ Δ mi* ((xi — Oц) 2 + yi 2 ). После ряда подстановок и упрощения выражения в итоге получится равенство Io = I + m*x i 2 — 2*m*xi 2 = I — m*xi 2 .
Так как x центра масс совпадает с d, расстоянием между осями, одну из которых можно направить через центр, то формулу можно переписать как Io = I — m*d 2 . Выразив из выражения произвольный момент, формула Штейнера примет вид I = Io + m*d 2 .
Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.
Пример задачи

Допустим, есть монета с массой m и радиусом r. Вращение происходит вокруг оси, распложенной по касательной. Необходимо найти момент вращения.
Для этого нужно знать характеристику прямой, пересекающей центр монеты Io. Решение будет определяться суммой Io и расстоянием от центра до касательной, которая равняется диаметру монеты: I = Io + md 2 . Фактически задача состоит в нахождении Io. Определяется этот параметр согласно теореме о взаимно перпендикулярных осях.
Момент вращения относительно диска определяется с помощью выражения I1 = m* d 2 / 2. Для решения задачи она будет выглядеть Io = m* d 2 / 4. Подставив все данные, получим: I = (1m*d2 / 4) + (md)2 = 5*m*d2 /4.
https://nauka.club/fizika/moment-inertsii.html