Расчет Эффективной ставки в EXCEL
Эффективная ставка возникает, когда имеют место Сложные проценты . Понятие эффективная ставка встречается в нескольких определениях. Например, есть Эффективная (фактическая) годовая процентная ставка, есть Эффективная ставка по вкладу (с учетом капитализации), есть Эффективная процентная ставка по потребительским кредитам . Разберемся, что эти ставки из себя представляют и как их рассчитать в MS EXCEL.
Эффективная (фактическая) годовая процентная ставка
В MS EXCEL есть функция ЭФФЕКТ(номинальная_ставка, кол_пер), которая возвращает эффективную (фактическую) годовую процентную ставку, если заданы номинальная годовая процентная ставка и количество периодов в году , в которые начисляются сложные проценты. Под номинальной ставкой здесь понимается, годовая ставка, которая прописывается, например, в договоре на открытие вклада. Предположим, что сложные проценты начисляются m раз в год. Эффективная годовая процентная ставка дает возможность увидеть, какая годовая ставка простых процентов позволит достичь такого же финансового результата, что и m-разовое наращение в год по ставке i/m, где i – номинальная ставка. При сроке контракта 1 год по формуле наращенной суммы имеем: S = Р*(1+i/m)^m – для сложных процентов, где Р – начальная сумма вклада. S = Р*(1+iэфф) – для простых процентов
Так как финансовый результат S должен быть, по определению, одинаков для обоих случаев, приравниваем оба уравнения и после преобразования получим формулу, приведенную в справке MS EXCEL для функции ЭФФЕКТ() iэфф =((1+i/m)^m)-1
Примечание . Если задана эффективная годовая процентная ставка, то величина соответствующей ей годовой номинальной процентной ставки рассчитывается по формуле
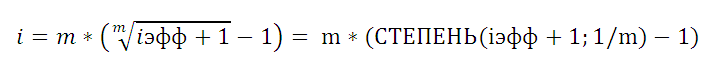
или с помощью функции НОМИНАЛ(эффективная_ставка, кол_периодов). См. файл примера .
Эффективная ставка по вкладу
Если договор вклада длится, скажем, 3 года, с ежемесячным начислением по сложным процентам по ставке i, то Эффективная ставка по вкладу вычисляется по формуле: iэфф =((1+i/12)^(12*3)-1)*(1/3) или через функцию ЭФФЕКТ( ): iэфф= ЭФФЕКТ(i*3;3*12)/3 Для вывода формулы справедливы те же рассуждения, что и для годовой ставки: S = Р*(1+i/m)^(3*m) – для сложных процентов, где Р – начальная сумма вклада. S = 3*Р*(1+iэфф) – для простых процентов (ежегодной капитализации не происходит, проценты начисляются раз в год (всего 3 раза) всегда на первоначальную сумму вклада). Если срок вклада =1 году, то Эффективная ставка по вкладу = Эффективной (фактической) годовой процентной ставке (См. файл примера ).
Эффективная процентная ставка по потребительским кредитам
Эффективная ставка по вкладу и Эффективная годовая ставка используются чаще всего для сравнения доходности вкладов в различных банках. Несколько иной смысл закладывается при расчете Эффективной ставки по кредитам, прежде всего по потребительским. Эффективная процентная ставка по кредитам используется для сравнения различные кредитных предложений банков. Эффективная процентная ставка по кредиту отражает реальную стоимость кредита с точки зрения заёмщика, то есть учитывает все дополнительные выплаты, непосредственно связанные с кредитом (помимо платежей по самому кредиту). Такими дополнительными выплатами являются банковские комиссии — комиссии за открытие и ведение счёта, за приём в кассу наличных денег и т.п., а также страховые выплаты. По закону банк обязан прописывать в договоре эффективную ставку по кредиту. Но дело в том, что заемщик сразу не видит кредитного договора и поэтому делает свой выбор, ориентируясь лишь на номинальную ставку, указанную в рекламе банка. Для создания расчетного файла в MS EXCEL воспользуемся Указаниями Центробанка РФ от 13 мая 2008 года № 2008-У «О порядке расчета и доведения до заемщика — физического лица полной стоимости кредита» (приведена Формула и порядок расчета эффективной процентной ставки), а также разъяснительным письмом ЦБ РФ № 175-Т от 26 декабря 2006 года, где можно найти примеры расчета эффективной ставки (см. здесь http://www.cbr.ru/publ/VesnSearch.aspx ). Эффективную ставку по кредиту рассчитаем используя функцию ЧИСТВНДОХ() . Для этого нужно составить график платежей по кредиту и включить в него все дополнительные платежи.
Пример . Рассчитаем Эффективную ставку по кредиту со следующими условиями: Сумма кредита — 250 тыс. руб., срок — 1 год, дата договора (выдачи кредита) – 17.04.2004, годовая ставка – 15%, число платежей в году по аннуитетной схеме – 12 (ежемесячно). Дополнительные расходы – 1,9% от суммы кредита ежемесячно, разовая комиссия – 3000р. при открытии банковского счета.
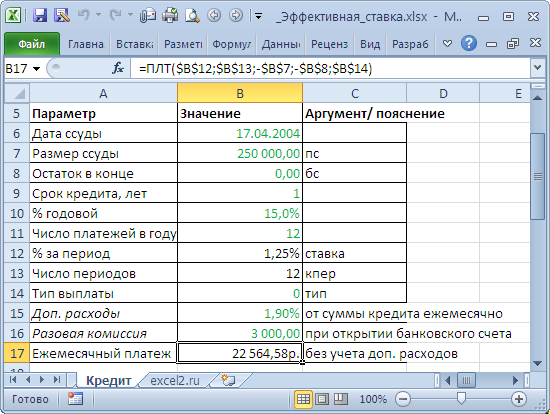
Сначала составим График платежей по кредиту с учетом дополнительных расходов (см. файл примера Лист Кредит ). Затем сформируем Итоговый денежный поток заемщика (суммарные платежи на определенные даты).
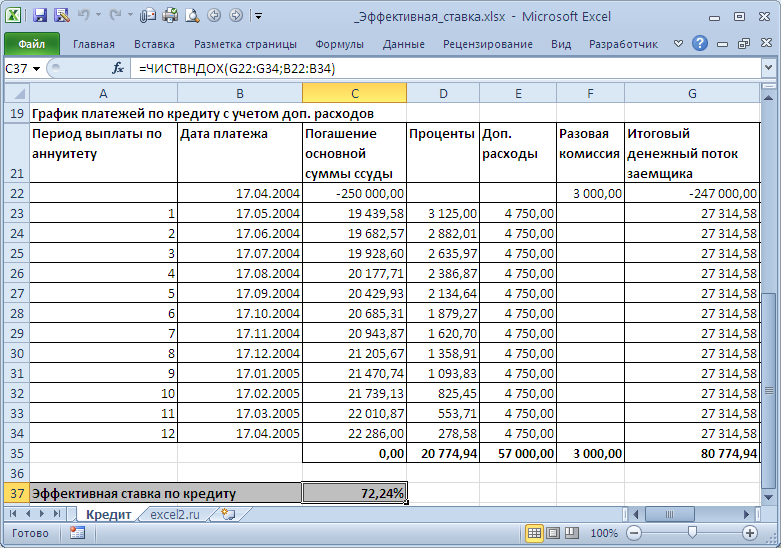
Эффективную ставку по кредиту iэфф определим используя функцию ЧИСТВНДОХ (значения, даты, [предп]). В основе этой функции лежит формула:
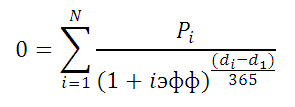
Где, Pi = сумма i-й выплаты заемщиком; di = дата i-й выплаты; d1 = дата 1-й выплаты (начальная дата, на которую дисконтируются все суммы).
Учитывая, что значения итогового денежного потока находятся в диапазоне G22:G34 , а даты выплат в B22:B34 , Эффективная ставка по кредиту для нашего случая может быть вычислена по формуле =ЧИСТВНДОХ(G22:G34;B22:B34) . Получим 72,24%. Значения Эффективных ставок используются при сравнении нескольких кредитов: чья ставка меньше, тот кредит и более выгоден заемщику. Но, что за смысл имеет 72,24%? Может быть это соответствующая ставка по простым процентам? Рассчитаем ее как мы делали в предыдущих разделах: Мы переплатили 80,77т.р. (в виде процентов и дополнительных платежей) взяв кредит в размере 250т.р. Если рассчитать ставку по методу простых процентов, то она составит 80,77/250*100%=32,3% (срок кредита =1 год). Это значительно больше 15% (ставка по кредиту), и гораздо меньше 72,24%. Значит, это не тот подход, чтобы разобраться в сути эффективной ставке по кредиту. Теперь вспомним принцип временной стоимости денег: всем понятно, что 100т.р. сегодня – это значительно больше, чем 100т.р. через год при 15% инфляции (или, наоборот — значительно меньше, если имеется альтернатива положить эту сумму в банк под 15%). Для сравнения сумм, относящихся к разным временным периодам используют дисконтирование, т.е. приведение их к одному моменту времени . Вспомнив формулу Эффективной ставки по кредитам, увидим, что для всех платежей по кредитам рассчитывается их приведенная стоимость к моменту выдачи кредита. И, если мы хотим взять в 2-х банках одну и туже сумму, то стоит выбрать тот банк, в котором получается наименьшая приведенная стоимость всех наших платежей в погашение кредита. Почему же тогда не сравнивают более понятные приведенные стоимости, а используют Эффективную ставку? А для того, чтобы сравнивать разные суммы кредита: Эффективная ставка поможет, если в одном банке дают 250т.р. на одних условиях, а в другом 300т.р. на других. Итак, у нас получилось, что сумма всех наших платежей в погашение основной суммы кредита дисконтированных по ставке 72,24% равна размеру кредита (это из определения эффективной ставки). Если в другом банке для соблюдения этого равенства потребуется дисконтировать суммы платежей идущих на обслуживание долга по б о льшей ставке, то условия кредитного договора в нем менее выгодны (суммы кредитов могут быть разными). Поэтому, получается, что важнее не само значение Эффективной ставки, а результат сравнения 2-х ставок (конечно, если эффективная ставка значительно превышает ставку по кредиту, то это означает, что имеется значительное количество дополнительных платежей: убрав файле расчета все дополнительные платежи получим эффективную ставку 16,04% вместо 72,24%!).
Примечание . Функция ЧИСТВНДОХ() похожа на ВСД() (используется для расчета ставки внутренней доходности, IRR ), в которой используется аналогичное дисконтирование регулярных платежей, но на основе номера периода выплаты, а не от количества дней.
Использование эффективной ставки для сравнения кредитных договоров с разными схемами погашения
Представим себе ситуацию, когда в 2-х разных банках нам предлагают взять в кредит одинаковую сумму на одинаковых условиях, но выплата кредита в одном будет осуществляться дифференцированными платежами , а в другом по аннуитетной схеме (равновеликими платежами). Для простоты предположим, что дополнительные платежи не взимаются. Зависит ли значение эффективной ставки от графика погашения? Сразу даем ответ: зависит, но незначительно.
В файле примера на листе Сравнение схем погашения (1год) приведен расчет для 2-х различных графиков погашения (сумма кредита 250 т.р., срок =1 год, выплаты производятся ежемесячно, ставка = 15%).
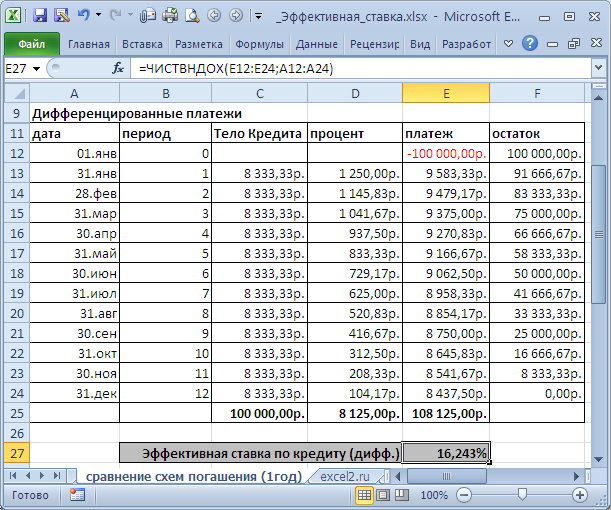
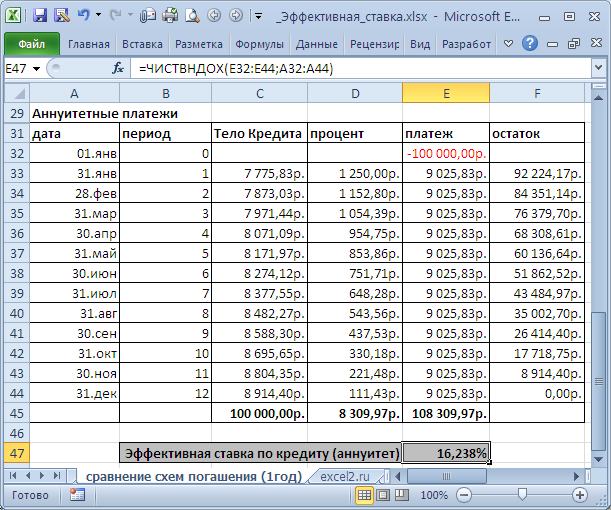
В случае дифференцированных платежей Эффективная ставка по кредиту = 16,243%, а в случае аннуитета – 16,238%. Разница незначительная, чтобы на ее основании принимать решение. Необходимо определиться какой график погашения больше Вам подходит.
При увеличении срока кредита разница между Эффективными ставками практически не изменяется (см. файл примера Лист Сравнение схем погашения (5лет) ).
Примечание . Эффективная годовая ставка, рассчитанная с помощью функции ЭФФЕКТ() , дает значение 16,075%. При ее расчете не используются размеры фактических платежей, а лишь номинальная ставка и количество периодов капитализации. Если грубо, то получается, что в нашем частном случае (без дополнительных платежей) отличие эффективной ставки по кредиту от номинальной (15%) в основном обусловлено наличием периодов капитализации (самой сутью сложных процентов).
Примечание . Сравнение графиков погашения дифференцированными платежами и по аннуитетной схеме приведено в этой статье .
Примечание. Эффективную ставку по кредиту можно рассчитать и без функции ЧИСТВНДОХ() — с помощью Подбора параметра. Для этого в файле примера на Листе Кредит создан столбец I (Дисконтированный денежный поток (для Подбора параметра)). В окне инструмента Подбор параметра введите значения указанные на рисунке ниже.
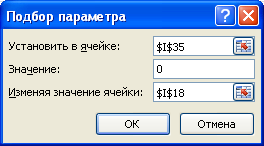
После нажатия кнопки ОК, в ячейке I18 будет рассчитана Эффективная ставка совпадающая, естественно, с результатом формулы ЧИСТВНДОХ() .
https://excel2.ru/articles/raschet-effektivnoy-stavki-v-ms-excel